《张朝阳的物理课》介绍量子力学

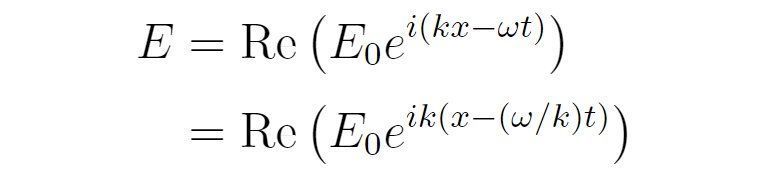
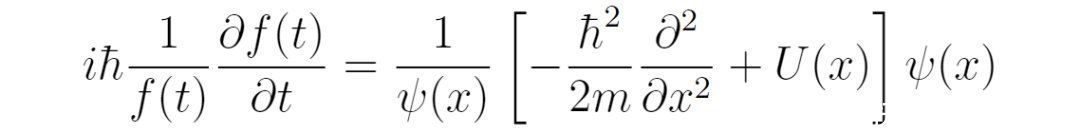
因此，只需要求出所有的ψ_E即可得到一般的波函数。ψ_E满足的方程为

说回光子，在宏观下它表现为电磁波，其电场分量可以描述为

希尔伯特空间 算符与平均值

接着，张朝阳介绍了“能量阶梯”的相关知识。不同类型的物理过程对应的特征能量标度存在数量级上的差异。比如化学变化所对应的能量标度为几个电子伏特，而核反应对应的能量标度可达兆电子伏特。能量标度的不同决定了各温度下的主要物理过程。比如室温下能发生的过程主要是化学过程，而要发生核聚变则需要达到百万开尔文的温度(注：原子核衰变是一个自发过程，即使在低温下也能发生)。正因为能量阶梯的存在，宇宙在大爆炸之后不断膨胀，温度不断降低，从而从高到低经历各个能量标度，这就决定了宇宙的物质形成是分阶段的。直到宇宙诞生38万年后，质子才捕获电子形成了原子。

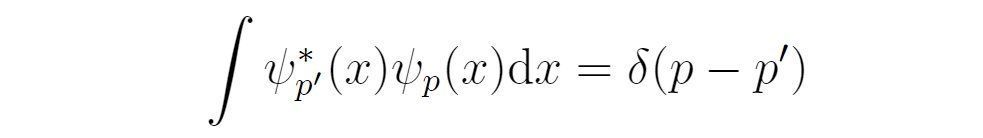
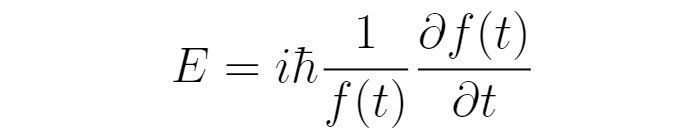
于是

这就是一维自由粒子的薛定谔方程。

单位基矢为

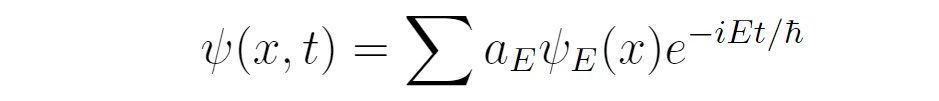
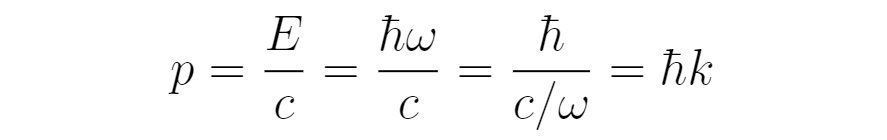
这个算符对应经典力学的哈密顿量，因此又被称为哈密顿算符。考虑了势能之后，薛定谔方程为

它作用在前述波函数上会得到对应动量与波函数的乘积。考虑非相对论的情况，且暂时不考虑势能，质量为m的粒子的能量为

对于黑体辐射，利用经典电磁理论得到的黑体辐射谱为

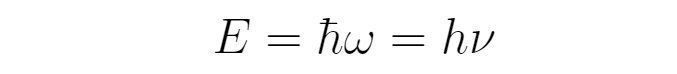
波函数的物理意义是什么呢？假如利用薛定谔方程求解得到波函数，能做出什么物理预言呢？这就涉及到量子力学的诠释了。目前物理学界的主要观点是统计诠释，波函数的模方等于测量粒子位置时测量结果的概率分布。因此，波函数需要满足归一化条件：波函数模方在全空间的积分等于1，代表的是在全空间内找到粒子的概率为1。可归一化是一个很强的条件，很多量子化的来源都是波函数的可归一性质。“波函数是一个单值的、处处连续的、可归一化函数”，总结成简单的口诀，就是波函数“单值、连续、可归一”

注意这里为方便，使用的是高斯单位制。当需要使用国际单位制时，只需在出现e^2处乘以库伦定律的比例系数即可。单位制的选择不影响讨论的结果。

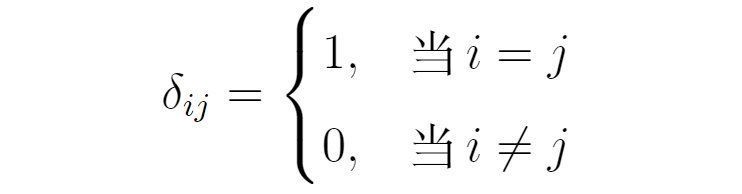
这样一组基被称为单位正交基。在这组单位正交基下，把位置矢量记为

所以

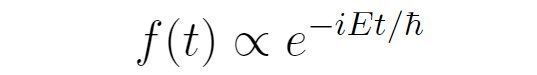
观察上式，可以定义动量算符，形式如下：

将其代入薛定谔方程，有

在其后的互动环节中，张朝阳还与现场听众探讨了各种物理问题。比如“在低能级的时候，系统的能量是离散的，但是能量高的时候，系统的能量表现为连续的，这是为什么呢？”为了解答这个问题，张朝阳以氢原子能级举例说明。氢原子的能量正比于-1/n^2，当氢原子处于低能级的时候，n很小，能量表现为离散的。当氢原子处于高能级时，n很大，虽然这时能量依然是离散的，但是能级之间的间隔趋于无穷小，因此能量表现为连续的。

于是，有

对于双原子分子气体，它有3个平动自由度，2个转动自由度，以及2个振动自由度，根据能量均分原理，单个分子的平均能量应该等于7kT/2，于是双原子分子气体的绝热指数为9/7。但是在室温下，双原子分子气体绝热指数的实验值约为1.4，经典理论值与实验值存在明显偏离。若考虑量子效应，双原子分子的固有频率很高，而谐振子能级间隔正比于固有频率，从而室温下振动自由度没有被激发，此时能量均分原理不适用于振动自由度。考虑这一点之后，双原子分子的平均能量为5kT/2，由此可以得到绝热指数为7/5=1.4，与实验值相符。

对于不同的E，会得到不一样的f(t)，以及不一样的波函数空间部分。因此，对波函数添加下标E以示区别。从而原来的波函数可写为

上一篇：核酸检测与流体力学 校园送餐与运筹学和控制论
下一篇：没有了